Cyrus-Beck算法是一种参数化裁剪算法,裁剪区域可以是平面上任意的凸多边形。被裁剪的直线采用参数化表达式:
$$
\textbf{P}(t) = \textbf{P}_0 + t(\textbf{P}_1 - \textbf{P}_0)
$$
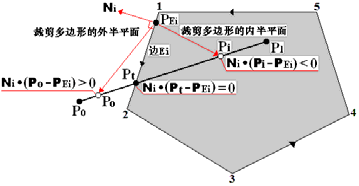
如图所示,通过计算点积$\textbf{N}_i \cdot (\textbf{P}(t) - \textbf{P}_{E_i})$的值,可知:
位于外半平面的点$\textbf{P}_0$有:$\textbf{N}_i \cdot (\textbf{P}_0 - \textbf{P}_{E_i}) > 0$;
位于内半平面的点$\textbf{P}_i$有:$\textbf{N}_i \cdot (\textbf{P}_i - \textbf{P}_{E_i}) < 0$;
在边上的点$\textbf{P}_t$有:$\textbf{N}_i \cdot (\textbf{P}_t - \textbf{P}_{E_i}) = 0$。
最后一个公式可代入直线的参数化表达式替换得到:
$$
t = - \dfrac{\textbf{N}_i \cdot (\textbf{P}_0 - \textbf{P}_{E_i})}{\textbf{N}_i \cdot \textbf{P}_0\textbf{P}_1}
$$
当上式除数不为0时,即可解得一个有效的t值。
首先,在区间[0,1]以外的t可以去掉,因为它位于线段$\textbf{P}_0\textbf{P}_1$之外。然后需要判断交点是否在裁剪边界上。如下图所示,4条线段中,线段a、b和d有2个交点供选择,线段c有4个交点供选择。
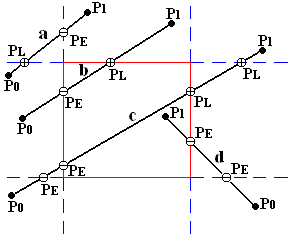
Cyrus-Beck算法采用的是如下原则去决定交点的类型,从而得到线段的可见部分:从被裁剪线段的端点$\textbf{P}_0$向$\textbf{P}_1$移动时,如果跨过一条边就进入该边所定义的内半平面,该交点就被定义为$P_E$;否则,该交点被定义为$P_L$。如果出现连续两个$P_E$则要取$t_E$大的一个;反之,出现连续两个$P_L$则要取$t_L$小的一个。
$P_E$和$P_L$区分的算法是:如果$\textbf{N}_i \cdot \textbf{P}_0\textbf{P}_1>0$,说明两者夹角小于$90^{\circ}$,定义为$P_L$,反之,如果$\textbf{N}_i \cdot \textbf{P}_0\textbf{P}_1<0$,说明两者夹角大于$90^{\circ}$,定义为$P_E$。
最后,$t_E$的下界是0,而$t_L$的上界是1,如果$t_E > t_L$意味着线段$\textbf{P}_0\textbf{P}_1$与裁剪多边形没有相交部分。有效交点的$t_E$和$t_L$将用来计算相应的x和y。伪代码如下:
