根据一维裁剪窗口与线段的左右两端点的坐标值大小,就能确定线段和裁剪窗口的可见部分,二维坐标系中计算裁剪窗口和线段的可见部分,也能如此转化,方法就是计算裁剪窗口延长线与线段所在直线的交点。当直线不与坐标轴平行时,一定与裁剪窗口的边所在的两对延长线存在交点。为了了解裁剪窗口和线段交点的情形,先确定一条直线$L_1(k>0)$,和裁剪窗口的纵坐标值$y_{min}$,$y_{max}$。假如所求线段$P_AP_B$在$L_1$沿$L_1$上下滑动,裁剪窗口沿水平方向左右滑动,则可以完全枚举出线段与裁剪窗口所有交点的情形,如下图所示。
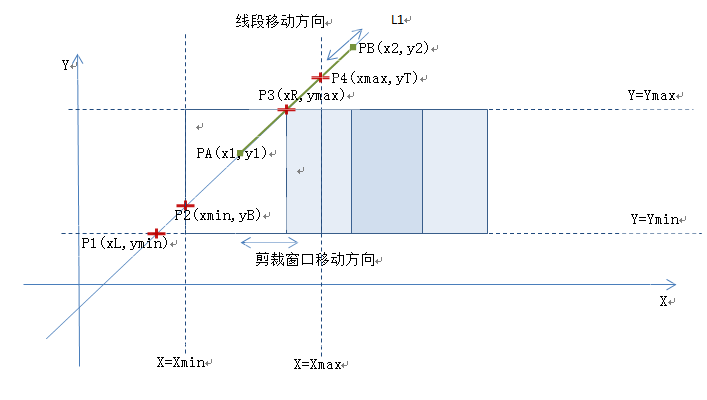
线段$L_1$的参数方程如下所示:
$$
\dfrac{x - x_1}{x_2 - x_1} = \dfrac{y - y_1}{y_2 - y_1} = u (0 \leq u \leq 1)
$$
设$\Delta x = x_2 - x_1$,$\Delta y = y_2 - y_1$,参数u在0~1之间取值,则线段上的任一点P(x, y)都可以满足下面的方程:
$$
x = x_1 + u(x_2 - x_1) = x_1 + u\Delta x \\
y = y_1 + u(y_2 - y_1) = y_1 + u\Delta y
$$
当点P位于由$(x_{min}, y_{min})$和$(x_{max}, y_{max})$所确定的裁剪窗口内满足下面不等式:
$$
x_{min} \leq x_1 + u\Delta x \leq x_{max} \\
y_{min} \leq y_1 + u\Delta y \leq y_{max}
$$
上面的不等式可以表示为:
$$
u \cdot r_k \leq q_k, k = 1, 2, 3, 4 \\
r_1 = -\Delta x, q_1 = x_1 - x_{min}, u_1 = \dfrac{q_1}{r_1} \\
r_2 = \Delta x, q_2 = x_{max} - x_1, u_2 = \dfrac{q_2}{r_2} \\
r_3 = -\Delta y, q_3 = y_1 - y_{min}, u_3 = \dfrac{q_3}{r_3} \\
r_4 = \Delta y, q_4 = y_{max} - y_1, u_4 = \dfrac{q_4}{r_4}
$$
其中,$r_1$与$r_2$符号相反,$r_3$与$r_4$符号相反。对于r=0的情形,表示线段$P_AP_B$平行于坐标轴,很容易确定它与裁剪窗口是否有公共部分。对于r不等于0的情形,当$r_k < 0$时,$u \geq \dfrac{q_k}{r_k}$,当$r_k > 0$时,$u \leq \dfrac{q_k}{r_k}$,则点P才能位于裁剪窗口内。同理,假如点P已经落在了裁剪窗口内,那么u一定大于等于所有$r_k < 0$时所对应的$u_k$的最大值,而小于等于所有$r_k > 0$时所对应的$u_k$的最小值。
参考: