复数
在我们能够完全理解四元数之前,我们必须先知道四元数是怎么来的。四元数的根源其实是复数。复数的集合$\mathbb{C}$是一个实数和一个虚数的和,形式如下:
$$
z = a + b\mathbf i \ a,b\in R,\ \mathbf i^{2} = -1
$$
如果$\mathbf i$的平方等于-1,那么$\mathbf i$的n次幂也应该存在:
$$
\mathbf i^{0} = 1
$$
$$
\mathbf i^{1} = \mathbf i
$$
$$
\mathbf i^{2} = -1
$$
$$
\mathbf i^{3} = \mathbf i\mathbf i^{2} = -\mathbf i
$$
你可能已经在数学里头见过类似的模式,但是是以(x,y,-x,-y,x,…)的形式,这是在2D笛卡尔平面对一个点逆时针旋转90度时生成的;(x,-y,-x,y,x,…)则是在2D笛卡尔平面对一个点顺时针旋转90度时生成的。我们也能够把复数映射到一个2D网格平面——复数平面,只需要把实数映射到横轴、虚数映射到纵轴。如前面的序列所示,我们可以认为,对一个复数乘以$\mathbf i$,这个复数就在复数平面上旋转了90度。
旋转数
我们也可以在复数平面上进行任意角度的旋转,只需要定义下面这个复数:
$$
q = cos\theta + \mathbf i sin\theta
$$
任意的复数乘以$q$:
$$
p = a + b\mathbf i
$$
$$
q = cos\theta + \mathbf i sin\theta
$$
$$
pq = (a + b\mathbf i)(cos\theta + \mathbf i sin\theta )
$$
$$
a’ + b’\mathbf i = acos\theta -bsin\theta + (asin\theta +bcos\theta )\mathbf i
$$
所以,对于每一个点$(a,b)$,$q$把它移动到了$(acos\theta -bsin\theta, asin\theta +bcos\theta)$的位置,也就是旋转了$\theta$。我们还可以把这个过程写成矩阵形式:
$$
R_{\theta} \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} acos\theta -bsin\theta \\ asin\theta +bcos\theta \end{pmatrix}
$$
为了更好地看出复数与矩阵的联系,我们可以把矩阵写成这样的形式:
$$
R_{\theta} = cos\theta \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} + sin\theta \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}
$$
其中,
$$
\mathbf1 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \mathbf i = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}
$$
于是,我们可以把每个复数都表示成矩阵的形式:
$$
\begin{pmatrix} a & -b \\ b & a \end{pmatrix} = a\mathbf1 + b\mathbf i, a,b\in R
$$
综上,在复数平面绕原点逆时针旋转任意点可写成:
$$
\begin{pmatrix} a’&-b’\\ b’&a’\\ \end{pmatrix} = \begin{pmatrix} cos\theta &-sin\theta \\ sin\theta &cos\theta \\ \end{pmatrix} \begin{pmatrix} a&-b\\ b&a\\ \end{pmatrix}
$$
四元数
了解了复数系统和复数平面后,我们可以额外增加2个虚数到我们的复数系统,从而把这些概念拓展到3维空间。对于四元数来说,这种『矩阵表示』的方法同样适用。每一个四元数$q$对应了一个矩阵:
$$
q = \begin{pmatrix} a+id & -b-ic \\ b-ic & a-id \end{pmatrix}
$$
(这并不是四元数与矩阵的唯一对应方法,但这种方法是复数与矩阵对应的推广。)
四元数的一般形式:
$$
q = a\mathbf1 + b\mathbf i + c\mathbf j + d\mathbf k
$$
其中,
$$
\mathbf1 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \mathbf i = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}, \mathbf j = \begin{pmatrix} 0 & -i \\ -i & 0 \end{pmatrix}, \mathbf k = \begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix}
$$
上面的公式是根据Hamilton的著名的表达式得到的:
$$
\mathbf i^{2} = \mathbf j^{2} = \mathbf k^{2} = \mathbf i\mathbf j\mathbf k = -1
$$
以及:
$$
\mathbf i \mathbf j = \mathbf k \ \ \ \mathbf j \mathbf k = \mathbf i \ \ \ \mathbf k \mathbf i = \mathbf j
$$
$$
\mathbf j \mathbf i = -\mathbf k \ \ \ \mathbf k \mathbf j = -\mathbf i \ \ \ \mathbf i \mathbf k = -\mathbf j
$$
$\mathbf i、\mathbf j、\mathbf k$虚数可以被用来表达3个笛卡尔坐标系单位向量。
我们可以用有序对的形式,来表示四元数:
$$
[w,\mathbf {v}] \ \ \ w\in \mathbb{R},v\in \mathbb{R^{3}}
$$
其中的$\mathbf v$,也可以用它各自独立的3个分量表示:
$$
q = [w,x\mathbf i + y\mathbf j + z\mathbf k] \ \ \ w,x,y,z\in \mathbb{R}
$$
和复数类似,四元数也可以被加减:
$$
q_{a} = [w_{a},\mathbf {a}]
$$
$$
q_{b} = [w_{b},\mathbf {b}]
$$
$$
q_{a} + q_{b} = [w_{a} + w_{b},\mathbf {a} + \mathbf {b}]
$$
$$
q_{a} - q_{b} = [w_{a} - w_{b},\mathbf {a} - \mathbf {b}]
$$
四元数的乘积:
$$
q_{a}q_{b} = [w_{a},\mathbf {a}][w_{b},\mathbf {b}] = [w_{a}w_{b} - \mathbf a\cdot \mathbf b, w_{a}\mathbf b + w_{b}\mathbf a + \mathbf a\times \mathbf b]
$$
共轭四元数的计算,就是将四元数的虚向量取反:
$$
q = [w,\mathbf {v}]
$$
$$
q^{*} = [w,-\mathbf {v}]
$$
四元数的模可以这样定义:
$$
|\mathbf q| = \sqrt {w^{2} + v^{2}}
$$
$$
\mathbf q\mathbf q^{*} = |\mathbf q|^{2}
$$
四元数的逆:
$$
\mathbf q^{-1} = \frac {\mathbf q^{*}}{|\mathbf q|^{2} }
$$
旋转
根据四元数和复数的相似性,应该有可能设计一个可以旋转3D空间的点的四元数:
$$
\mathbf q = [cos\theta, sin\theta \mathbf {v}]
$$
让我们测试一下这个理论是否可靠,方法就是计算四元数$q$和向量$\mathbf p$的积。第一步,我们把$\mathbf p$写成纯四元数的形式:
$$
\mathbf p = [0,\mathbf {p}]
$$
以及单位四元数$q$:
$$
\mathbf q = [s,\lambda \mathbf {\hat { \mathbf v }}]
$$
从而:
$$
\mathbf p’ = \mathbf q\mathbf p = [s,\lambda \mathbf {\hat { \mathbf v }}] [0,\mathbf {p}] = [-\lambda \mathbf {\hat { \mathbf v }}\cdot \mathbf {p}, s\mathbf {p} + \lambda \mathbf {\hat { \mathbf v }}\times \mathbf {p} ]
$$
我们可以看到结果是一个同时有系数、有虚向量的四元数。然而,Hamilton发现,如果对$\mathbf q\mathbf p$右乘$q$的逆,出来的结果是一个纯四元数,并且四元数向量部分的模可以保持不变。为了正确地让一个向量绕某个轴向量旋转某个角度,我们必须以目标角度的一半来计算。因此,我们构造了下面的四元数:
$$
q = [cos\frac {1}{2}\theta ,sin\frac {1}{2}\theta \mathbf { \hat { \mathbf v } }]
$$
这就是旋转四元数的一般形式。
旋转四元数的证明
我们想要证明的是,给定$t=cos\theta + usin\theta$,其中$u$是$\mathbb{R} \mathbf{i} + \mathbb{R} \mathbf{j} + \mathbb{R} \mathbf{k}$中单位向量,那么$t$的共轭作用将把$\mathbb{R} \mathbf{i} + \mathbb{R} \mathbf{j} + \mathbb{R} \mathbf{k}$绕着$u$所在的轴$\mathbb{R}u$旋转$2\theta$。
证明分两步,首先我们证明$\mathbb{R}u$是旋转轴。这也就意味着,我们要证明$u$的所有实数倍的向量在$t$的共轭作用下保持原位:
$$
\begin{aligned}
tut^{-1} &= (cos\theta + usin\theta)u(cos\theta - usin\theta) \\
&= (ucos\theta + u^2sin\theta)(cos\theta - usin\theta) \\
&= (ucos\theta - sin\theta)(cos\theta - usin\theta) \\
&= u(cos^2\theta + sin^2\theta) - sin\theta cos\theta - u^2sin\theta cos\theta \\
&= u
\end{aligned}
$$
接下来,我们在$\mathbb{R} \mathbf{i} + \mathbb{R} \mathbf{j} + \mathbb{R} \mathbf{k}$中选取垂直于$u$的单位向量$v$,令$w=u \times v$。于是,${u,v,w}$是$\mathbb{R} \mathbf{i} + \mathbb{R} \mathbf{j} + \mathbb{R} \mathbf{k}$的一组规范正交基。
为了证明确实旋转了$2\theta$,我们只需要证明$tvt^{-1} = vcos2\theta + wsin2\theta$以及$twt^{-1} = wcos2\theta - vsin2\theta$就好了。两者证明类似,这里只证明前者:
$$
\begin{aligned}
tvt^{-1} &= (cos\theta + usin\theta)v(cos\theta - usin\theta) \\
&= (vcos\theta + uvsin\theta)(cos\theta - usin\theta) \\
&= vcos^2\theta - vusin\theta cos\theta + uvsin\theta cos\theta - uvusin^2\theta \\
&= vcos^2\theta + 2uvsin\theta cos\theta + u^2vsin^2\theta \\
&= v(cos^2\theta - sin^2\theta) + 2wsin\theta cos\theta \\
&= vcos2\theta + wsin2\theta
\end{aligned}
$$
证明完毕!
还有一种直观的证明方法。如图所示,$\mathbb{R}u$为旋转轴,旋转角度为$\sigma$,向量$\mathbf v$旋转到$\mathbf w$处。旋转到$\dfrac{\sigma}{2}$处为$\mathbf k$(图中未标出)。
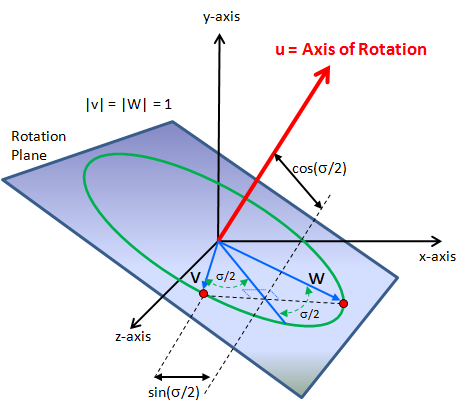
首先,令$u$方向上的单位向量为$\mathbf u$(为了方便,命名不变,后面的$\mathbf u$都是指旋转轴方向的单位四元数),那么根据$q$的定义,参见四元数乘法法则:
$$
q=(\cos{\frac{\theta}{2}},\mathbf{u}\sin{\frac{\theta}{2}}) = (\mathbf{v}\cdot \mathbf{k},\mathbf{v}\times\mathbf{k})=(0,\mathbf{k})(0,-\mathbf{v})=\mathbf k \mathbf v^*
$$
现在令
$$
w=qvq^{-1}
$$
如果能证明$\mathbf w$与$\mathbf v$的夹角是$\sigma$,那么就说明$\mathbf w$确实是$\mathbf v$旋转$\sigma$得到的,整个命题就得证了。
注意$\mathbf v$,$\mathbf k$和$\mathbf w$都是实部为0的单位四元数,表示单位向量,我们有:
$$
wk^*=(qvq^{-1})k^*=qvq^*k^*=qvvk^*k^*=q
$$
所以
$$
wk^*=kv^*
$$
上面的式子拆分成实部和虚部,虚部表明$\mathbf w$与$-\mathbf k$的平面和$\mathbf k$与-$\mathbf v$的平面重合,实部表明$\mathbf w$和$-\mathbf k$之间的夹角与$\mathbf k$和-$\mathbf v$之间的夹角相等,都是$\pi - \dfrac{\sigma}{2}$。这就说明了$\mathbf w$与$\mathbf v$的夹角是$\sigma$,原命题就得证了。
参考:
1.https://www.zhihu.com/question/23005815
2.https://www.zhihu.com/question/41485992