默认状态下,Direct3D认为顶点排列顺序为顺时针(观察坐标系中)的三角形单元是正面朝向的,顶点排列顺序为逆时针(观察坐标系中)的三角形单元是背面朝向的。
那么,如何判断一个三角形的绕序呢?让我们先从三角形的基本性质看起。
在左手坐标系中,当从三角形“正面”看时,经常以顺时针方向列出这些点,设这三个顶点为$v_1、v_2、v_3$。让我们标出下图中的三角形内角、顺时针边向量、边长。
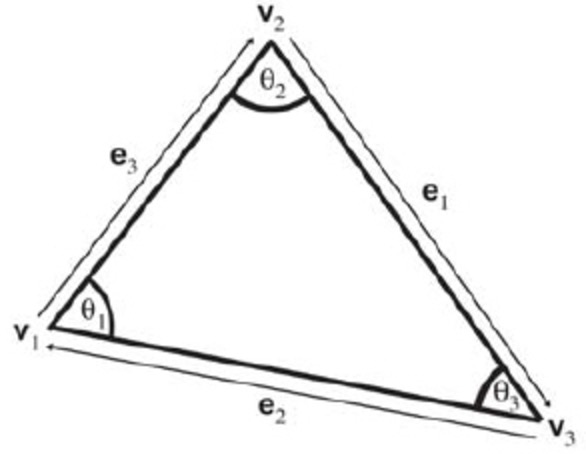
设$l_i$为$e_i$的长度,注意$e_i、l_i$和$v_i$的对应关系,$v_i$为相应下标的顶点,它们的关系如下:
$$
e_1 = v_3 - v_2 \quad l_1 = |e_1| \\
e_2 = v_1 - v_3 \quad l_2 = |e_2| \\
e_3 = v_2 - v_1 \quad l_3 = |e_3|
$$
由正弦定理可知:
$$
\dfrac{sin\theta_1}{l_1} = \dfrac{sin\theta_2}{l_2} = \dfrac{sin\theta_3}{l_3}
$$
由余弦定理可知:
$$
l_1^2 = l_2^2 + l_3^2 - 2l_2l_3cos\theta_1 \\
l_2^2 = l_1^2 + l_3^2 - 2l_1l_3cos\theta_2 \\
l_3^2 = l_1^2 + l_2^2 - 2l_1l_2cos\theta_3
$$
接下来我们来看下三角形的面积。
如果不知道高,可以使用海伦公式计算面积,它只需要提供三边的长度即可。设s为周长的一半(也称作半周长),公式如下:
$$
s = \dfrac{l_1 + l_2 + l_3}{2} = \dfrac{p}{2} \\
A = \sqrt{s(s - l_1)(s - l_2)(s - l_3)}
$$
海伦公式非常有用,因为它在3D中使用非常方便。
有时候,高和周长都没有直接提供,所知道的只有顶点的笛卡尔坐标。(当然,总是可以从坐标中算出边长,但在某些情况下,我们想要避免这种代价相对较高的计算。)让我们看看能否从顶点坐标直接计算面积。
先在2D中解决这个问题。基本思想是,对三角形三边中的每一边,计算上由该边,下由x轴所围成的梯形的有符号面积。
有符号面积是指:如果边的端点是从左向右的,则面积为正;如果边的端点是从右向左的,则面积为负。注意不管三角形的方向如何变化,都存在至少一个正边和一个负,一个竖直边的面积为0。各边下面区域的面积分别为:
$$
A(e_1) = \dfrac{(y_3 + y_2)(x_3 - x_2)}{2} \\
A(e_2) = \dfrac{(y_1 + y_3)(x_1 - x_3)}{2} \\
A(e_3) = \dfrac{(y_2 + y_1)(x_2 - x_1)}{2}
$$
即使一部分(或整个)三角形扩展到了x轴下边,上面的公式依然正确。这三个梯形的有符号面积相加,就得到了三角形本身的面积。事实上,能用同样的思想计算任意多边形的面积。
这里,假设顶点是按顺指针列出的,如果顶点以相反的顺序列出,面积的符号将变负。将这三个梯形的面积相加,计算三角形的有符号面积:
$$
\begin{align}
A &= A(e_1) + A(e_2) + A(e_3) \\
&= \dfrac{y_1(x_2 - x_3) + y_2(x_3 - x_1) + y_3(x_1 - x_2)}{2}
\end{align}
$$
实际上,还能进一步简化。基本思想是,平移三角形不会改变三角形的面积。因此,我们可以在竖直方向上平移三角形,从每个y坐标中减去$y_3$,如下所示。(用代数变换也能得到这个简化形式。)
$$
A = \dfrac{(y_1 - y_3)(x_2 - x_3)+ (y_2 - y_3)(x_3 - x_1)}{2}
$$
在3D中,可以通过叉乘来计算三角形的面积。两向量a、b叉乘的大小等于以a、b为两边的平行四边形的面积。因为三角形面积等于包围它的平行四边形的一半,所以我们有了一种简便方法。给出三角形的两个边向量,$e_1$和$e_2$,则三角形面积为:
$$
A = \dfrac{|e_1 \times e_2|}{2}
$$
综上,我们可以通过计算三角形的有符号面积来判断三角形的绕序。若面积为正,则为顺时针绕序,否则即为逆时针绕序。要注意有符号面积的计算应当是在透视除法后计算,这样可以确保与z无关。
在观察坐标系中,还有一种很直观的办法可以判断三角形的绕序:
1、按约定顺序(顺时针)计算出两个边向量:
$$
\overrightarrow{v_1} = (x_3 - x_2, y_3 - y_2, z_3 - z_2) \\
\overrightarrow{v_2} = (x_1 - x_3, y_1 - y_3, z_1 - z_3)
$$
2、求两个边向量的叉乘,得到面法向量:
$$
\overrightarrow{n} = \overrightarrow{v_1} \times \overrightarrow{v_2}
$$
3、计算视线向量$\overrightarrow{view}$,可以取三角形面上任意点减去相机的坐标则该向量是从三角形面指向相机的。但可以采取简单做法:在观察坐标系中相机坐标即为原点坐标。
4、求面法向量与视线向量的点积,如果点积大于0,说明夹角为锐角,是正面,即顺时针绕序,否则即为逆时针绕序。