透视投影是3D固定流水线的重要组成部分,是将相机空间中的点从视锥体(frustum)变换到规则观察体(Canonical View Volume)中,待裁剪完毕后进行透视除法的行为。在算法中它是通过透视矩阵乘法和透视除法两步完成的。
经过相机矩阵的变换,顶点被变换到了相机空间。这个时候的多边形也许会被视锥体裁剪,但在这个不规则的体中进行裁剪并非那么容易的事情,所以裁剪被安排到规则观察体(Canonical View Volume, CVV)中进行,多边形裁剪就是用这个规则体完成的。所以,事实上是透视投影变换由两步组成:
1) 用透视变换矩阵把顶点从视锥体中变换到裁剪空间的CVV中
2) CVV裁剪完成后进行透视除法
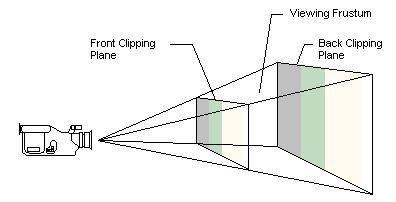
视锥体是一个三维体,它的位置和摄像机相关,视锥体的形状决定了模型如何从camera space投影到屏幕上。透视投影使得离摄像机近的物体投影后较大,而离摄像机较远的物体投影后较小。透视投影使用棱锥作为视锥体,摄像机位于棱锥的椎顶。该棱锥被前后两个平面截断,形成一个棱台,叫做View Frustum,只有位于Frustum内部的模型才是可见的。
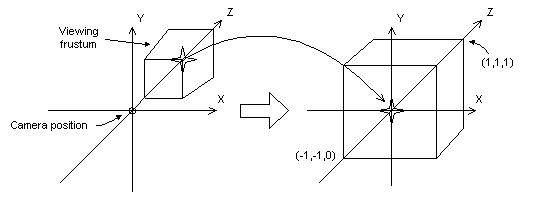
透视投影的目的就是将上面的棱台转换为一个立方体(cuboid),转换后,棱台的前剪裁平面的右上角点变为立方体的前平面的中心(下图中弧线所示)。由图可知,这个变换的过程是将棱台较小的部分放大,较大的部分缩小,以形成最终的立方体。这就是投影变换会产生近大远小的效果的原因。变换后的x坐标范围是[-1, 1],y坐标范围是[-1, 1],z坐标范围是[0, 1](OpenGL略有不同,z值范围是[-1, 1])。
为了简化问题,我们考虑YOZ平面上的投影情况,见下图。设P(x, y, z)是Frustum内一点,它在近剪裁平面上的投影是P’(x’, y’, z’)。(注意:D3D以近剪裁平面作为投影平面),设视锥体在Y方向的夹角为$\theta$。
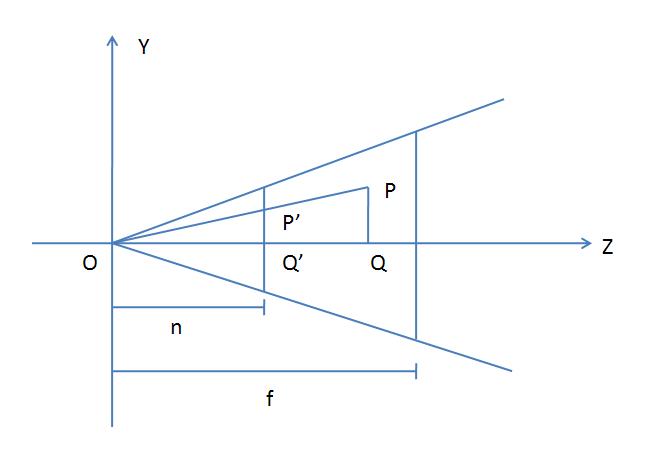
由三角形相似可知:
$$
\dfrac{P_y}{y’} = \dfrac{P_z}{n}
$$
故有$y’ = \dfrac{nP_y}{P_z}$,同理有$x’ = \dfrac{nP_x}{P_z}$,$z’ = n$。
接下来,我们要把点P’进行缩放,在x和y方向把顶点从Frustum情形变成CVV情形。将P’缩放的过程,假设投影平面的高度为H,由于转换后cuboid的高度为2。所以有:
$$
\dfrac{y’}{y’’} = \dfrac{H}{2}
$$
故有$y’’ = \dfrac{2y’}{H} = \dfrac{2nP_y}{HP_z}$,因为$cot\theta = \dfrac{2n}{H}$,所以最终得到:
$$
y’’ = \dfrac{P_y}{P_z}cot\theta
$$
同理,又因为投影平面的宽高比为Aspect,有:
$$
x’’ = \dfrac{2x’}{W} = \dfrac{2nP_x}{WP_z} = \dfrac{2nP_x}{HAspectP_z} = \dfrac{P_x}{P_z} cot\theta \dfrac{1}{Aspect}
$$
最后看z’’。当Frustum内的点投影到近剪裁平面的时候,实际上这个z’值已经没有意义了,因为所有位于近剪裁平面上的点,其z’值都是n,不过由于需要进行深度测试,在光栅化之前,我们需要对z坐标的倒数进行插值,所以可以将z’’写成z的一次表达式形式,如下:
$$
z’’ = a\dfrac{1}{P_z} + b
$$
写成这样的形式,主要有以下三个原因:
- 后面投影之后的光栅化阶段,要通过x’’和y’’对z进行线性插值,以求出三角形内部片元的z,进行z缓冲深度测试。在数学上,投影后的x’’和y’’,与z不是线性关系,与1/z才是线性关系。而a/z+b正是1/z的线性关系。用这个1/z的线性组合值和x’’、y’’进行插值才是正确的。
- P’的3个代数分量统一地除以分母z,易于使用齐次坐标变为普通坐标来完成,使得处理更加一致、高效。
- 后面的CVV是一个规则体,便于进行多边形裁剪。而我们可以适当地选择系数a和b,使得这个式子在z = n的时候值为0,而在z = f的时候值为1,从而在z方向上构建CVV。
所以,我们可得到下列方程组:
$$
\begin{cases}
0 = a\dfrac{1}{n} + b \\
1 = a\dfrac{1}{f} + b
\end{cases}
$$
解方程,得到:
$$
\begin{cases}
a = \dfrac{fn}{n-f} \\
b = \dfrac{f}{f-n}
\end{cases}
$$
代入可求出z’’:
$$
z’’ = \dfrac{fn}{n - f} \dfrac{1}{P_z} + \dfrac{f}{f-n}
$$
最终投影点P’的齐次坐标(x’’,y’’,z’’, 1)为
$$
(\dfrac{P_x}{P_z} cot\theta \dfrac{1}{Aspect}, \dfrac{P_y}{P_z}cot\theta, \dfrac{fn}{n - f} \dfrac{1}{P_z} + \dfrac{f}{f-n}, 1)
$$
下面要做的就是从这个新形式出发反推出透视投影矩阵。注意到
$(\dfrac{P_x}{P_z} cot\theta \dfrac{1}{Aspect}, \dfrac{P_y}{P_z}cot\theta, \dfrac{fn}{n - f} \dfrac{1}{P_z} + \dfrac{f}{f-n}, 1)$是
$(P_x cot\theta \dfrac{1}{Aspect}, P_y cot\theta, \dfrac{fn}{n - f} + \dfrac{f}{f-n}P_z, P_z)$经过透视除法的形式,所以我们做透视除法的逆处理——给P’每个分量乘上z,得到
$$
(P_x, P_y, P_z, 1)M = (P_x cot\theta \dfrac{1}{Aspect}, P_y cot\theta, \dfrac{fn}{n - f} + \dfrac{f}{f-n}P_z, P_z)
$$
最终得到投影矩阵为:
$$
M = \begin{bmatrix}
\dfrac{cot\theta}{Aspect} & 0 & 0 & 0 \\
0 & cot\theta & 0 & 0 \\
0 & 0 & \dfrac{f}{f - n} & 1 \\
0 & 0 & \dfrac{fn}{n - f} & 0
\end{bmatrix}
$$
M就是最终的透视变换矩阵。相机空间中的顶点,如果在视锥体中,则变换后就在CVV中。如果在视锥体外,变换后就在CVV外。而CVV本身的规则性对于多边形的裁剪很有利。注意到M的最后一列不是(0 0 0 1)而是(0 0 1 0),因此可以看出透视变换不是一种仿射变换,它是非线性的。
另外一点,对于投影面来说,它的宽和高大多数情况下不同,即宽高比不为1,比如640/480。而CVV的宽高是相同的,即宽高比永远是1。这就造成了多边形的失真现象,比如一个投影面上的正方形在CVV的面上可能变成了一个长方形。解决这个问题的方法就是在对多变形进行透视变换、裁剪、透视除法之后,在归一化的设备坐标(Normalized Device Coordinates)上进行的视口(viewport)变换中进行校正,它会把归一化的顶点之间按照和投影面上相同的比例变换到视口中,从而解除透视投影变换带来的失真现象。进行校正前提就是要使投影平面的宽高比和视口的宽高比相同。
参考: