在流水线中,当物体从模型坐标通过世界矩阵变换到世界空间之后,它将通过相机变换从世界空间变换到相机空间。所谓的相机空间,就是以相机作为坐标原点的一个参考系,所以,从世界空间变换到相机空间,就是把物体从世界坐标系,变换到相机为原点的相机坐标系,如图所示。
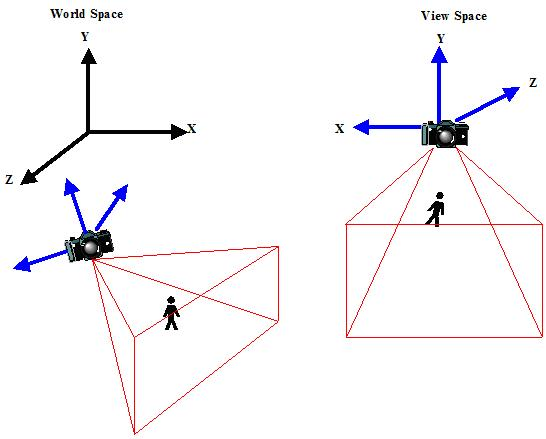
左半部分是小人在世界空间中的位置,右半部分是小人变换到相机空间后的位置。这里我们讨论最为广泛的UVN系统构建观察矩阵。
UVN系统
UVN系统本身是一个基。如下图所示,三个基向量U,V,N分别指向相机的右方、上方和后方从而构成右手坐标系,相机则处于坐标原点。
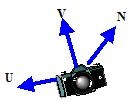
在参考系下(这里是世界坐标系),我们给定相机的位置——eye,被观察的小人的位置——lookat,以及一个辅助向量——参考系中表示“上方”的向量up,这个向量会影响U和V的生成,因为以后求出的V向量会在up和N向量所决定的平面上,所以可以通过这个向量让相机产生不同的偏转。
首先我们求出向量$\overrightarrow{N}$:
$$
\overrightarrow{N} = lookat - eye
$$
然后,我们求出向量$\overrightarrow{U}$。这一步需要使用辅助向量up,如果不希望相机产生偏转,一般取(0, 1, 0):
$$
\overrightarrow{U} = \overrightarrow{up} \times \overrightarrow{N}
$$
U使用向量的叉乘实现。最后,使用N和U计算出向量$\overrightarrow{V}$:
$$
\overrightarrow{V} = \overrightarrow{N} \times \overrightarrow{U}
$$
最后将计算出的$\overrightarrow{U}$,$\overrightarrow{V}$和$\overrightarrow{N}$进行单位化,就得到了相机的UVN系统。我们可以把UVN系统看作是相机的基,从而可以方便地把一个向量在世界坐标和相机坐标进行转换。
观察矩阵推导
由变换过程可知,物体是先随着观察坐标系平移至世界坐标系,然后旋转使得观察坐标系与世界坐标系完全重合。所以总的变换分为两部分:平移+旋转。可写作:
$$
C=TR
$$
首先,平移变换很容易求出:
$$
T =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
T_x & T_y & T_z & 1
\end{bmatrix}
$$
经过平移后,相机的原点和世界原点就重合了。通过旋转,将此时的观察坐标系与世界坐标系重合,因为点随着观察坐标系一起旋转,因此这相当于将观察坐标系中的某个点坐标(x, y, z)旋转变换到世界坐标系下的相同坐标表示(x, y, z)。从而我们有:
$$
(x, y, z) \begin{bmatrix} \overrightarrow{U} \\ \overrightarrow{V} \\ \overrightarrow{N} \end{bmatrix} \cdot R = (x, y, z)
$$
也可理解为将观察坐标系的基底经过旋转变换转换为世界坐标系的基底,同样有:
$$
\begin{bmatrix} \overrightarrow{U} \\ \overrightarrow{V} \\ \overrightarrow{N} \end{bmatrix} \cdot R = I
$$
所以旋转变换其实是$\begin{bmatrix} \overrightarrow{U} \\ \overrightarrow{V} \\ \overrightarrow{N} \end{bmatrix}$的逆矩阵。而因为该矩阵是正交的,所以逆矩阵即为其转置矩阵:
$$
R = \begin{bmatrix} \overrightarrow{U} \overrightarrow{V} \overrightarrow{N} \end{bmatrix} = \begin{bmatrix}
U_x & V_x & N_x & 0 \\
U_y & V_y & N_y & 0 \\
U_z & V_z & N_z & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
$$
故观察矩阵为:
$$
C = TR = \begin{bmatrix}
U_x & V_x & N_x & 0 \\
U_y & V_y & N_y & 0 \\
U_z & V_z & N_z & 0 \\
\overrightarrow{T} \cdot \overrightarrow{U} & \overrightarrow{T} \cdot \overrightarrow{V} & \overrightarrow{T} \cdot \overrightarrow{N} & 1
\end{bmatrix}
$$
参考: