本文只考虑绕坐标轴旋转的旋转矩阵推导。这里以绕X轴旋转为例,左手坐标系。
假设三维坐标系中的某一向量$\overrightarrow{v}$,其在直角坐标系中的图如图1所示。
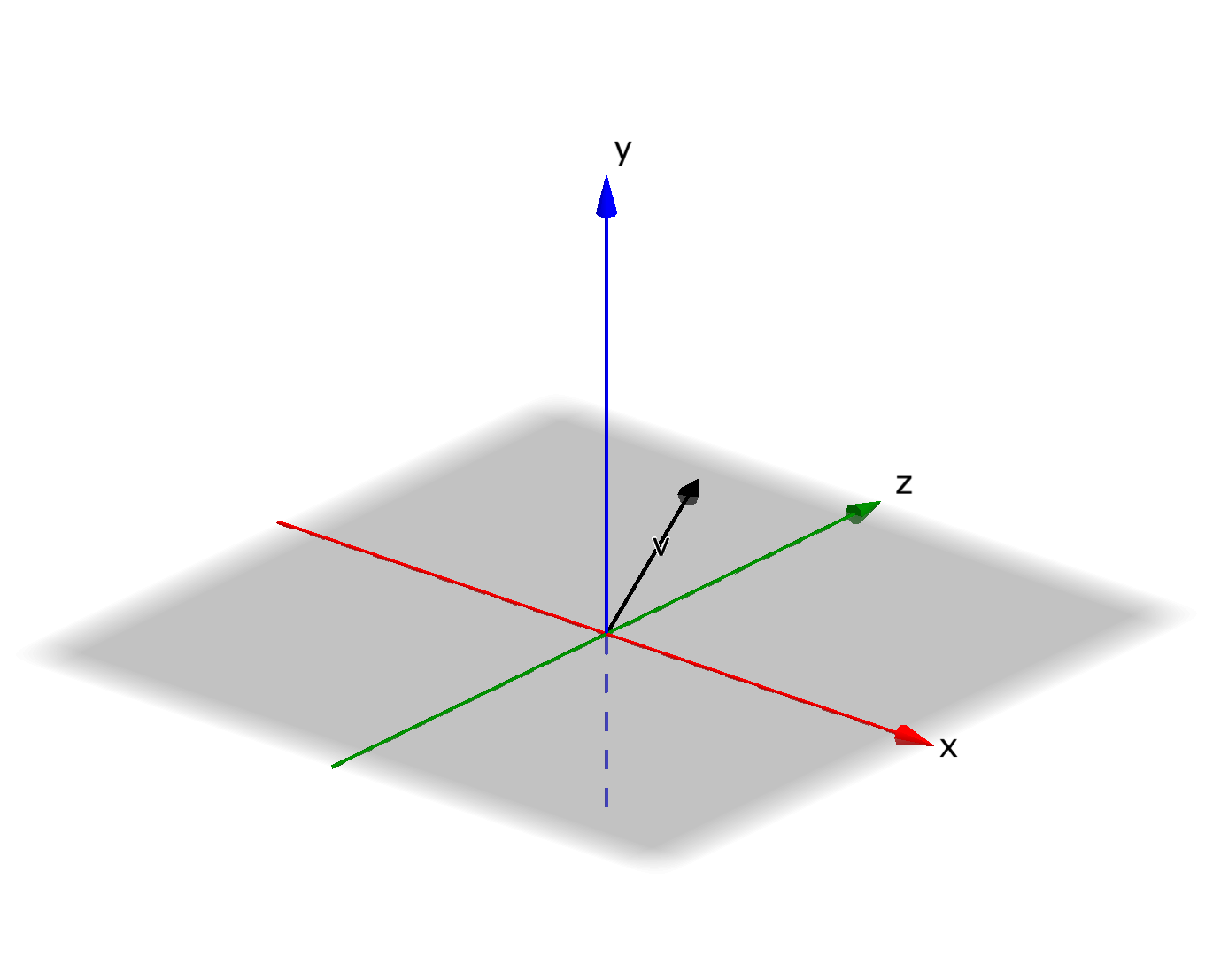
绕X轴旋转,相当于向量$\overrightarrow{v}$在YZ平面的投影$\overrightarrow{u}$绕原点旋转,如下图所示。注意,当沿着旋转轴指向原点的方向观察时,角度是按顺时针方向度量的。
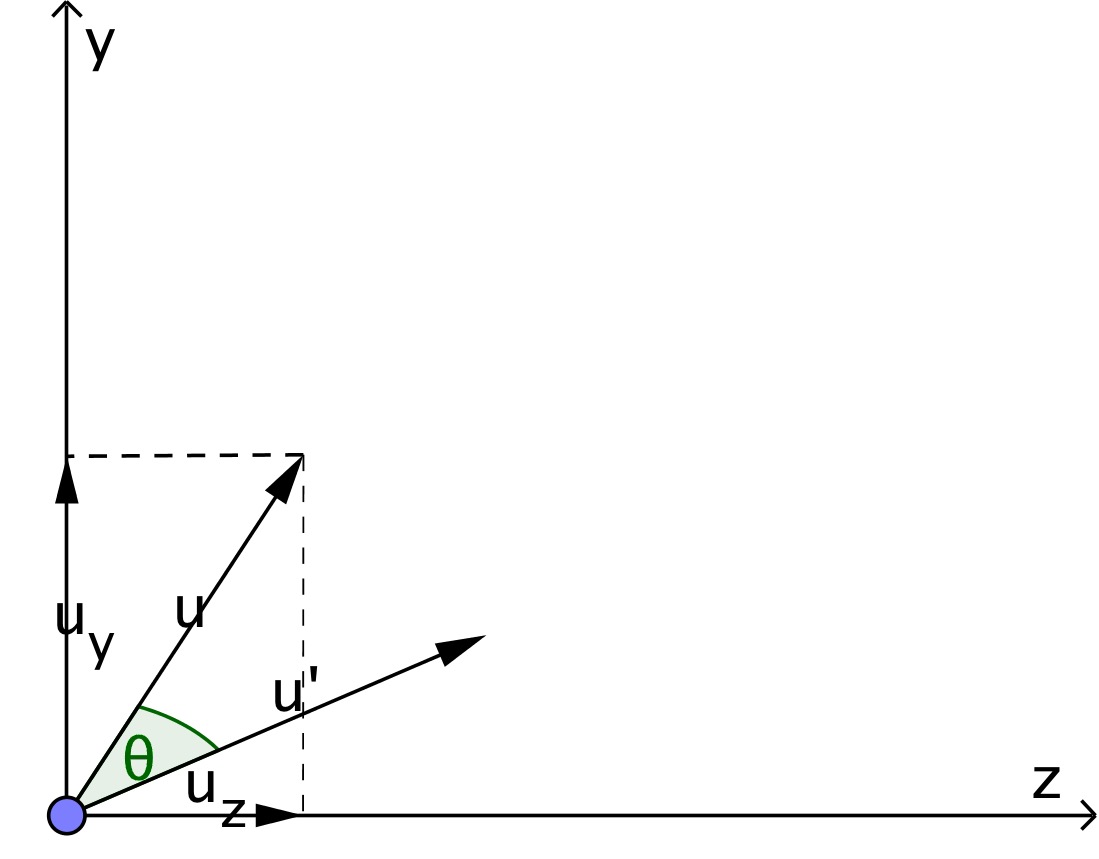
这里,为了求出旋转矩阵,即需要求出旋转后的向量$\overrightarrow{u’}$。可以将$\overrightarrow{u}$分解为坐标轴z方向的向量$\overrightarrow{u_z}$与y方向的向量$\overrightarrow{u_y}$。
然后,通过求出旋转后的向量分量$\overrightarrow{u_z’}$和$\overrightarrow{u_y’}$,就可以得到最终要求的向量$\overrightarrow{u’}$。
假设$\overrightarrow{u}$的坐标为($y$, $z$),易知$\overrightarrow{u_y’}$的坐标为($ycos\theta$, $ysin\theta$),$\overrightarrow{u_z’}$的坐标为($-zsin\theta$, $zcos\theta$)。
所以$\overrightarrow{u’}$的坐标为($ycos\theta-zsin\theta$, $ysin\theta+zcos\theta$)。
故绕X轴旋转的旋转矩阵为
$
R(x) =
\begin{bmatrix}
1 & 0 & 0 \\
0 & cos\theta & sin\theta \\
0 & -sin\theta & cos\theta
\end{bmatrix}
$。
此外,从另外一个观点来看,也可以保持向量固定来旋转坐标系。通过将坐标系绕X轴逆时针旋转,在原坐标系中的向量将顺时针旋转到新的位置。这样同样也可推出旋转矩阵。
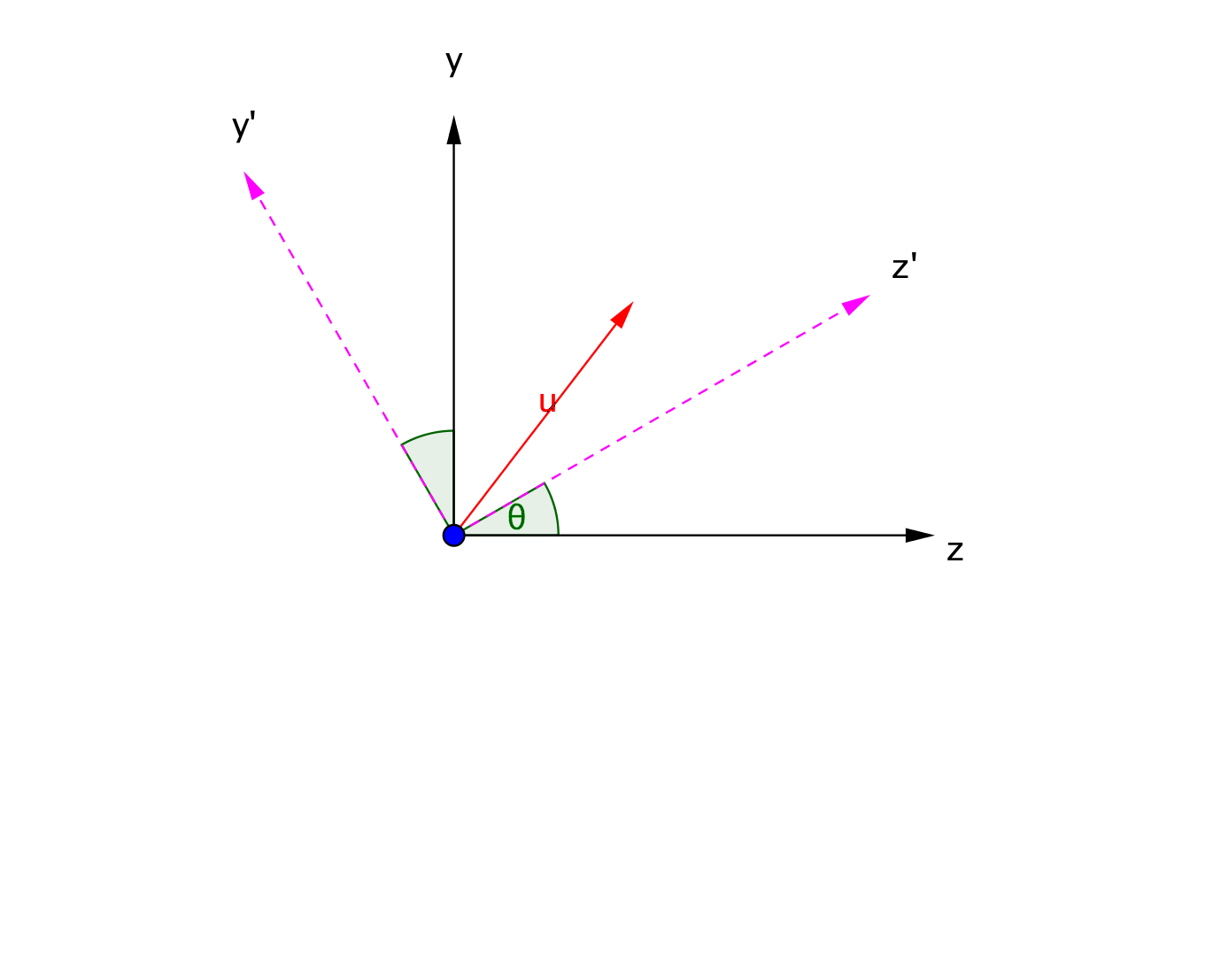
这里,假设原始向量$\overrightarrow{u}$ 的坐标为($y$, $z$),它的基底分别为原始的y轴和z轴,记为$\overrightarrow{N_y}$和$\overrightarrow{N_z}$。则,我们有:
$$
\overrightarrow{u} = y\overrightarrow{N_y} + z\overrightarrow{N_z} = (y, z) \begin{bmatrix} \overrightarrow{N_y} \\ \overrightarrow{N_z} \end{bmatrix}
$$
接下来我们来求逆时针旋转$\theta$角度后的基底$\overrightarrow{N_y’}$和$\overrightarrow{N_z’}$。得到:
$$
\overrightarrow{N_y’} = \overrightarrow{N_y}cos\theta - \overrightarrow{N_z}sin\theta
$$
$$
\overrightarrow{N_z’} = \overrightarrow{N_y}sin\theta + \overrightarrow{N_z}cos\theta
$$
假设旋转后的向量$\overrightarrow{u}$的坐标为($y’$, $z’$),则有:
$$
(y, z) \begin{bmatrix} \overrightarrow{N_y} \\ \overrightarrow{N_z} \end{bmatrix} = (y’, z’) \begin{bmatrix} \overrightarrow{N_y’} \\ \overrightarrow{N_z’} \end{bmatrix} = (y’, z’) \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} \overrightarrow{N_y} \\ \overrightarrow{N_z} \end{bmatrix}
$$
可以发现我们要求的旋转矩阵实际上为$\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$的逆矩阵。而因为该矩阵为正交矩阵,所以其逆矩阵即为转置矩阵,故最终得到绕X轴旋转的旋转矩阵为$R(x) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\theta & sin\theta \\ 0 & -sin\theta & cos\theta \end{bmatrix}$。
同理也可推出其他绕坐标轴旋转的矩阵。这里略去推导直接给出结果:
$
R(y) =
\begin{bmatrix}
cos\theta & -sin\theta & 0 \\
0 & 1 & 0 \\
sin\theta & 0 & cos\theta
\end{bmatrix}
$,
$
R(z) =
\begin{bmatrix}
cos\theta & sin\theta & 0 \\
-sin\theta & cos\theta & 0 \\
0 & 0 & 1
\end{bmatrix}
$。